Soms is het interessant om grafiekjes te kunnen bekijken. We laten uiteraard het eigenlijke werk, het tekenen van de grafiek, over aan iemand anders, en gebruiken een spreadsheet. Een voorbeeldje vind je in het programma zoekboomdiepte.cpp. Dit maakt een grafiek (wat die betekent zien we later, en slaat deze op in een bestand dieptedata.csv. Als je het programma laat lopen en dan dieptedata.csv inleest in je favoriete spreadsheet, zoals Excel of OpenOffice Calc, dan kan je met de diagramfunctie een grafiekje tekenen. Opmerking: dieptedata.csv is geschikt voor rekenbladprogramma's met een niet-Engelstalige instelling, waarbij vlottendekommagetallen worden voorgesteld met een vlottende komma. Hoe je een .csv-bestand produceert waar de vlottende komma vervangen is door een punt, vind je in de API van de klasse CsvData:

De klasse CsvData wordt gedefinieerd in de header csv.h Elk object van de klasse komt overeen met één .csv-bestand, waarin getalwaarden worden opgeslagen. Vermits de meeste rekenbladen grafieken kunnen opmaken met verschillende gegevensreeksen, waarbij elke gegevensreeks standaard opgeslagen is in een kolom, slaat elke CsvData gegevens ook op deze manier op. De API is de volgende

Binaire bomen kunnen door omstandigheden een zeer grote diepte bereiken. Een manier om dit te beperken is gebruik te maken van splayoperaties. Programmeer een afgeleide zoekboom (de oorspronkelijke boom zit in zoekboom.h, de nieuwe boom steek je in splayboomb.h, waarbij de eind-b bottom-up aanduidt) met een toevoegfunctie waarin splayen wordt gebruikt, en vergelijk de grafiek met deze van een gewone zoekboom. Je zal ook de hoofding puntgenerator.h nodig hebben.

Bijkomende opgave:
Gegeven twee binaire bomen die dezelfde sleutels bevatten, dan kan je de ene boom in de andere transformeren door rotaties uit te voeren. Maak een functie

Binboom<Sleutel,Data>::kopieerstructuur(Binboom<Sleutel,Data>&)

die controleert of het argument wel degelijk dezelfde sleutels bevat en, zoja, *this dezelfde structuur geeft als het afrument.

Rood-zwarte bomen zijn altijd nogal evenwichtig. Je betaalt er wel een prijs voor: toevoegen en verwijderen is ingewikkeld. Voor we ze implementeren zijn hier een paar toepassingen om op papier op te lossen.

De eerste oefening maakt duidelijk dat top-down- en bottom-upmethodes niet altijd hetzelfde resultaat opleveren. Bekijk de kleine boom.

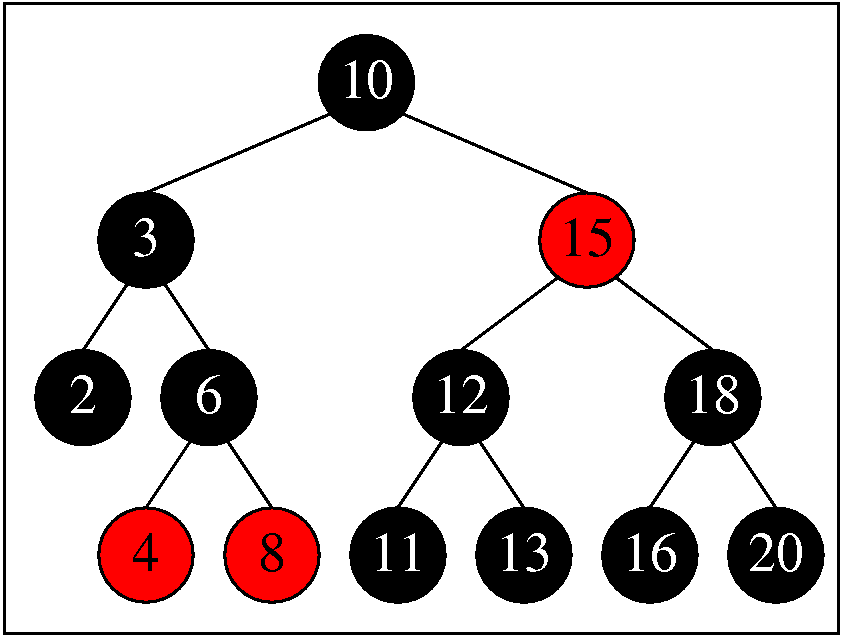
Verwijder de knoop met sleutel 8. Probeer het eerst bottom-up, daarna top-down. Verwijder ook eens 15: eerst bottom-up, dan top down.

Bij de tweede oefening hebben we een zeer scheve boom:

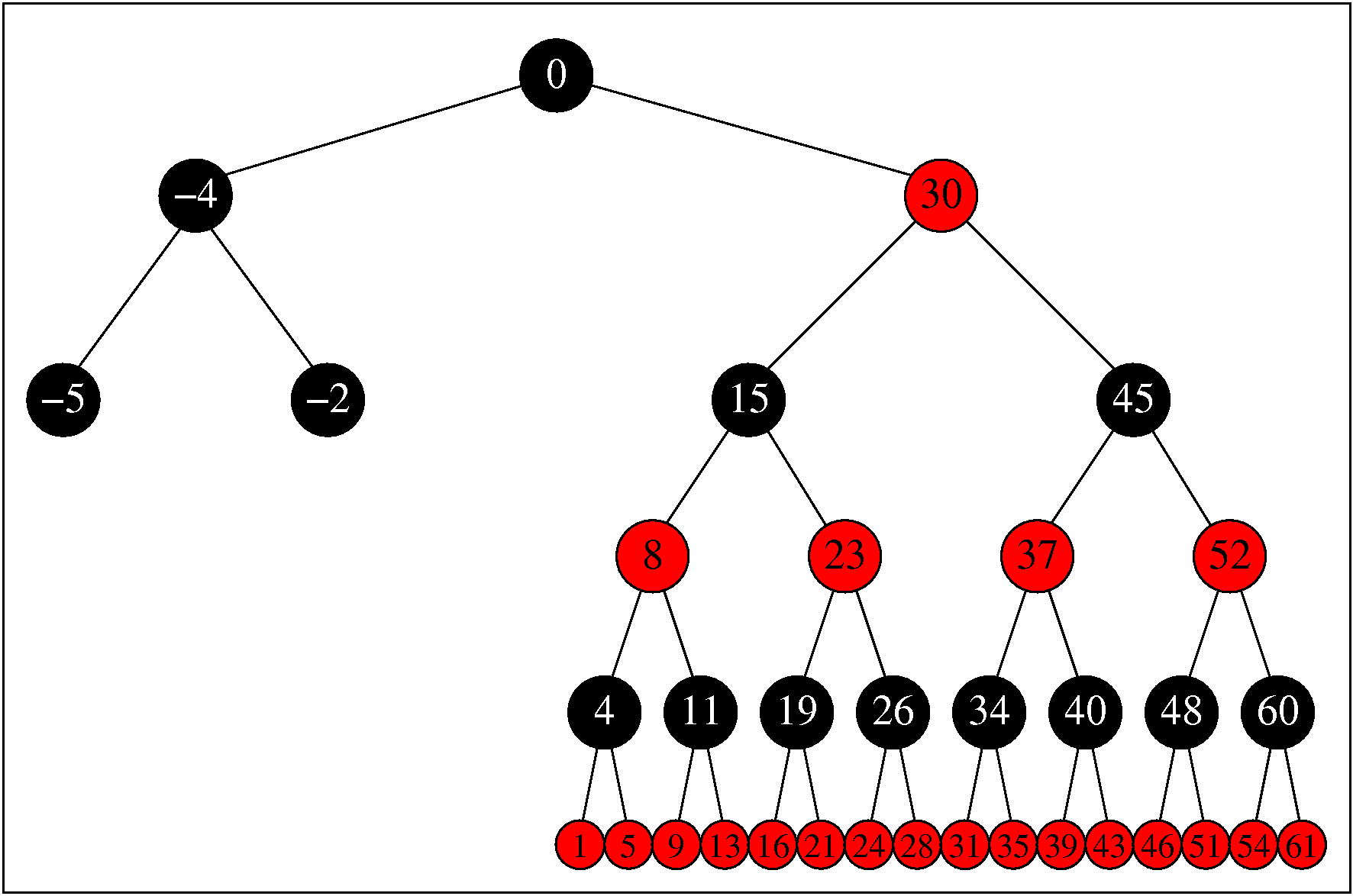
als l de diepte aan de linkerkant is, en r de diepte aan de rechterkant, dan is

Slechter kan niet bij een rood-zwarte boom, en elke bewerking zal de situatie verbeteren. Probeer maar: elke keer vertrekkend van de beginsituatie van de tekening moet je

• sleutel 6 bottom-up toevoegen.
• sleutel -2 top-down verwijderen.

Bijkomende opgave: een doordenkertje.

Een rood-zwarte boom is altijd nogal evenwichtig. Dat betekent dat je bij een willekeurige zoekboom niet altijd de knopen zo kan inkleuren dat je een rood-zwarte boom krijgt.

• Hoe kan je van een zoekboom uitvinden of je hem als rood-zwarte boom kan inkleuren, en hoe kleur je hem dan in?
• Door rotaties kan je een boom evenwichtiger maken, en er zo voor zorgen dat je hem rood-zwart kan inkleuren.